Summary
The relative
loudness of different size pipe bands strongly depends on how far away they are
from a listener. For a listener a long distance away, a band with ten times as many
bagpipers as another will sound twice as loud. If instead the bands are
marching close by the listener, although both will be absolutely louder, now
more than two hundred times the number of bagpipers are
required to sound twice as loud.
For the purposes of the analysis, we
assume that the bagpipers are playing the same tune with similar instruments;
the complications of drums are not included. First we will consider the effect
of increasing the number of bagpipers in a band – Size -
and then investigate the way the loudness varies as the band marches by – Distance.
Size The loudness perceived by a
listener depends both on the intensity level of the sound and the way their ear
and brain work to register it. While the sound intensity level can be readily
measured, the workings of the ear and brain fall in the realm of psychophysics
and are not completely understood 1
. However from extensive measurements, e.g. [2], most people
perceive loudness to scale with sound intensity to the power of approximately
0.3, i.e. if the sound intensity increases by a factor of 10, the listener
perceives the loudness to have increased by a factor of 2 (as 100.3 ~ 2). Formerly, the
change in loudness = n0.3
, where n is the ratio
of the two sound sources, or, in our case, band sizes.
The graph in Figure 1 shows the consequences of this
relationship between loudness and sound intensity, plotting the variation in
perceived loudness with the number of bagpipers, where all the players are
assumed to be grouped close together, at a long distance from the listener,
i.e. the band is perceived as a single point source of sound. When the band is
a long distance away, ten bagpipers will sound twice as loud as one, and one
hundred will sound four times as loud. Alternatively, increasing the band size
from ten to twenty pipers will increase the loudness perceived by a distant
listener by (20/10)0.3
=
1.23, i.e. it will be just 23% louder.
Distance
Sound intensity varies inversely with the square of the distance 3 , i.e.
doubling the distance between the sound source and the listener will reduce its
intensity by a factor of four; likewise at three times the distance, the sound
is reduced by a factor of nine. Knowing that perceived loudness scales with intensity
to the power of approximately 0.3, we have the rule of thumb that reducing your
distance away from a band by a factor of three will double its perceived
loudness, since (3 * 3)0.3 ~ 2.
To
begin investigating the effect of varying the distance between the listener and
the band, we can make some simplifying assumptions about the layout of the
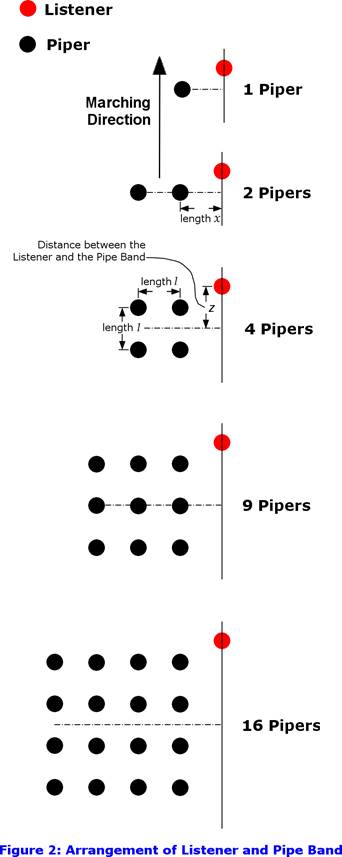
band. Figure 2 illustrates some symmetrical band
layouts of 1, 2, 4, 9 and 16 pipers, and a listener; the pipers are shown as
black circles, and the listener is a red circle. For each band, the distance
between the pipers in each rank and file is the same, the length l. Also we begin by analyzing the situation
where the band is marching close past the listener, with the file passing
within a length x = l, the same distance as between the
ranks and files. After this, we show the effect of the listener moving away
from the band, in units of this same length l.
With this
simple layout of the bands, it is relatively easy to calculate the loudness
perceived by the listener as the band marches by; we can sum up the sound
intensity of each piper, discounting their contribution by the square of their
distance from the listener. For example, at the instant when the 2-piper band
is in line with the listener, the left piper will be twice the distance from
the listener as the right one, so will contribute just one quarter of the sound
intensity. As the band moves away, the corresponding distances are readily
calculated (using Pythagoras’ theorem 4), the sound
intensities summed and converted to perceived loudness. We can also extend the
analysis for symmetrical band layouts of 25, 36 and 49 pipers (with ranks of 5,
6 and 7 pipers, respectively).
Figure 3
shows the variation in perceived loudness for different band sizes, as the band
marches away from the listener; the results are normalized to the loudness of
one piper a distance x = l from the
listener, marching from right by the piper, z
= 0,
to a long distance away, z =24. For the
1-piper band, (the blue curve), the relative perceived loudness ranges from 1,
at z = 0, to 0.148 at z = 24. For the
49-piper band (the purple curve), the relative perceived loudness drops to 0.474 at z
= 24.
Note that the ratio of these two, comparing the loudness of the 49-piper band
with the 1-piper band, at a long distance, z
=24
is
(0.474/0.148) = 3.2 ~ (49/1)0.3, i.e. agreeing with the result from
Figure 1.
However,
when the bands are close to the listener, the 49-piper band is no longer so
much louder, proportionally, than the 1-piper band. Of course, it is louder in
absolute terms; from Figure 3,
the purple curve rises to 1.64 times
louder, at z = 0. This decrease in relative loudness
for the larger band is simply because many of the pipers are relatively distant
from the listener. When the whole band is a long distance away, the listener
hears all pipers at approximately the same sound intensity; when the band is
close up, the nearest pipers are louder, but those in the further files, and the distant ends of the ranks are proportionally
quieter.
Figure
4 shows this
same effect, but instead graphing the perceived loudness against the number of
pipers, at the instant they 
pass the listener, at their maximum
loudness, z = 0; in this case the different curves
correspond to the listener moving away at right angles to the direction of
marching, from x = 1 to
x = ∞, in the direction marked in Figure 2. The distant curve (light-blue),
when the bands are a long distance from the listener, is the same as Figure 1, with the loudness increasing in
proportion to n0.3. The
1-length curve (blue), where the bands are just 1 length away from the
listener, shows the loudness increases much more slowly with number of pipers,
with the curve approximately proportional to n0.13. The curves in between these two extremes have
exponents of n ranging between these
values, approximately 0.13 to 0.3.
As an
example, from Figure
4, with the
listener 2 lengths away from the bands (red curve) as they marched past, (e.g. if the rank and file spacing is 7’6”, then the listener would be as
close as 15’ away), then a 25-piper
band would have a loudness of 1.86,
and a 4-piper band a loudness of 1.36; the perceived loudness of larger band would
be (1.86/1.36) = 1.37, i.e. 37% louder, even though there were (25 – 4) = 21 more pipers.
Figures
3 and 4 illustrate that the perceived
loudness of a band depends strongly on the listener’s distance away. Both
because our hearing perceives loudness as varying sub-linearly with sound
intensity, and also because this intensity falls off as the square of distance,
when we are near a large band, we only need to move a small distance away
before we perceive its loudness to be the same as one closer but much smaller;
for example, after listening to a 4-piper band passing one length away, and then
stepping back one additional length (perhaps to get a better view), a passing
25-piper band will be perceived as having approximately the same loudness.
Richard J.S
Bates
June 2014